x4
x4
2x4
2x3
x4
x4
=-2
x6 0
4x$ 2x6= 1
2x5 x6 3
xs
2.0000
-1.0000
0.0
1.0000
2.0000
1.0000
0.0
-1.0000
1.0000
-2.0000
1.0000
-1.0000
0.0
1.0000
0.0
-2.0000
3.0000
3.0000
2.0000
0.0
-2.0000
1.0000
1.0000
3.0000
2.0000
1.0000
1.0000
0.0
2.0000
-1.0000
2.0000
1.0000
4.0000
2.0000
1.0000
1.0000
0.0
0.0
1.0000
2.0000
1.0000
3.0000
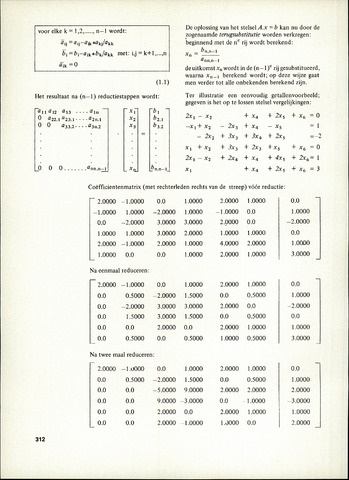
Na eenmaal reduceren:
2.0000
-1.0000
0.0
1.0000
2.0000
1.0000
0.0
0.0
0.5000
-2.0000
1.5000
0.0
0.5000
1.0000
0.0
-2.0000
3.0000
3.0000
2.0000
0.0
-2.0000
0.0
1.5000
3.0000
1.5000
0.0
0.5000
0.0
0.0
0.0
2.0000
0.0
2.0000
1.0000
1.0000
0.0
0.5000
0.0
0.5000
1.0000
0.5000
3.0000
Na twee maal reduceren
2.0000
-1.0000
0.0
1.0000
2.0000
1.0000
0.0
0.0
0.5000
-2.0000
1.5000
0.0
0.5000
1.0000
0.0
0.0
-5.0000
9.0000
2.0000
2.0000
2.0000
0.0
0.0
9.0000
-3.0000
0.0
-1.0000
-3.0000
0.0
0.0
2.0000
0.0
2.0000
1.0000
1.0000
0.0
0.0
2.0000
-1.0000
1.0000
0.0
2.0000
voor elke k 1,2,n—1 wordt:
ai> ^ij—"ik *^kj/^kk
b{ j—üfjk*Z>k/akk met: ij k+l,...,n
flik =0
De oplossing van het stelsel A.x b kan nu door de
zogenaamde terugsubstitutie worden verkregen:
beginnend met de ne rij wordt berekend:
^n.n 1
(1.1)
Het resultaat na (n—1) reductiestappen wordt:
all al2 fl13 a\n
0 Ü22.1 ü23.1 a2n.l
0 0 a33.2 fl3n.2
^nn.n—1
deuitkomstJcn wordt in de (n—l)e rij gesubstitueerd,
waarna xn_t berekend wordt; op deze wijze gaat
men verder tot alle onbekenden berekend zijn.
Ter illustratie een eenvoudig getallenvoorbeeld;
gegeven is het op te lossen stelsel vergelijkingen:
*1
~bi -
X2
b2.i
*3
b 3.2
- *IL
bn.n—1_
2x
X2
-X] x2
2x2
X! X2
2xj x2
X,
- 2x3
3x3
3x3
2x4
2x5 x6 0
0 0 0 ^nn.n—
Coëfficientenmatrix (met rechterleden rechts van de streep) vóór reductie:
1
- x 5
2x5
312